(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
Pythonで学ぶデータサイエンス入門:統計編第15回です.
前回までの記事で,\(x\)と\(y\)の2変数に対して線形回帰を実行し回帰直線\(y=a+bx\)を求めました.
最小二乗法により,回帰係数\(b\)と切片\(a\)はそれぞれ以下のようになるんでしたね!
$$a=\bar{y}-b\bar{x}$$
$$b=r\frac{s_y}{s_x}$$
さて,身長から体重を予測する回帰直線を求めたとしましょう.その回帰直線って,身長から体重を予測するのにも使えるのでしょうか?
どういうことかというと,前回の記事で,ある体重と身長のデータセットに対して線形回帰をしたところ,\(y=-37.95+0.58x\)という回帰直線が求まったわけですが,この式は身長\(x\)から体重\(y\)を予測する式として使えるんでした.
でもこれって,体重\(y\)を代入して,身長\(x\)を求めて,体重から身長を予測することもできそうですよね?
実はこれはできません.回帰直線の間違った使い方になります.
今回はこの辺りを解説したいと思います.
目次
xからyを予測する回帰直線でyからxは予測できない??
先ほどの例で,身長から体重を予測する回帰直線\(y=-37.95+0.58x\)は,体重から身長を予測する際にも使えるか?
答えはNoです.
まぁ,もちろん普通に体重\(y\)を代入して身長\(x\)が求まるっちゃもとまるんですが,それは最適な予測値ではありません.
体重\(y\)から身長\(x\)を予測する回帰直線\(x=a’+b’y\)を求めると,前回の記事から\(a’\)と\(b’\)は以下のようになるのは明白だと思います(xとyを入れ替えただけ)
$$a’=\bar{x}-b’\bar{y}$$
$$b’=r\frac{s_x}{s_y}$$
これは,\(y=a+bx\)に以下の値を代入した式とは違う式になります.(興味がある人は計算してみてください.)
$$a=\bar{y}-b\bar{x}$$
$$b=r\frac{s_y}{s_x}$$
これは言い換えると,説明変数と目的変数を入れ替えると,別の回帰直線ができあがるわけです.
Pythonでふた通りの回帰直線を描画してみる
前回まで使っていたデータで二通りの回帰直線を求めて描画してみましょう!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline weight = np.array([42, 46, 53, 56, 58, 61, 62, 63, 65, 67, 73]) height = np.array([138, 150, 152, 163, 164, 167, 165, 182, 180, 180, 183]) # reg1: heightからweightを予測する回帰直線 X = np.expand_dims(height, axis=-1) y = weight reg1 = LinearRegression() reg1.fit(X, y) # reg2: weightからheightを予測する回帰直線 X = np.expand_dims(weight, axis=-1) y = height reg2 = LinearRegression() reg2.fit(X, y) # 直線を描画するためのx軸の値リストを作成 x = np.arange(130, 190, 1) # 学習に使った値を散布図で描画 plt.scatter(height, weight) # reg1を描画 plt.plot(x, x*reg1.coef_+reg1.intercept_, 'b') # reg2を描画(x=a'+b'yを変形し,y=(x-a')/b')となることに注意 plt.plot(x, (x-reg2.intercept_)/reg2.coef_, 'r') #reg1とreg2が交差している点がweightとheightの平均の点 plt.plot(np.mean(height), np.mean(weight), 'ro') plt.xlabel('height') plt.ylabel('weight') |
少し長くなってしましましたが,前回の記事でちゃんと回帰直線を求めていたら理解できると思います.
横軸height, 縦軸weightの座標系に描画するために,二つ目の回帰直線は\(x=a’+b’y\)と考え,これを変形して\(y=(x-a’)/b’\)として描画することに注意しましょう.
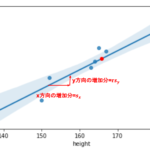
上のコードを実行すると以下のような図が描画できると思います.
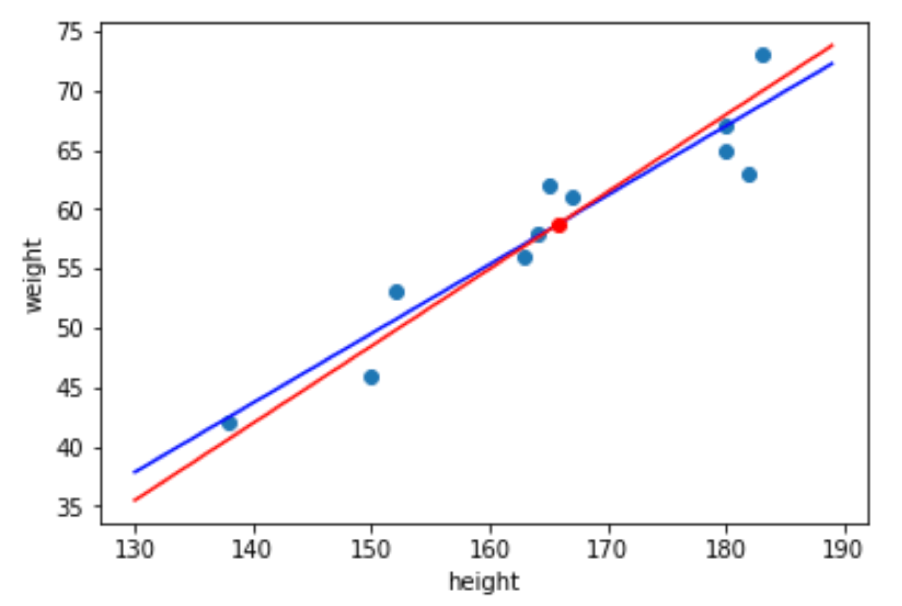
青い線が身長から体重を予測する回帰直線で,赤い線が体重から身長を予測する回帰直線です.
微妙にずれてますね!笑
どちらの回帰直線も点\((\bar{x}, \bar{y})\)を通るので,\((\bar{x}, \bar{y})\)で交わっています.
どちらを目的変数にとるかで回帰直線の結果が変わるので注意しましょう.当たり前のようですが,色々データをいじってその過程で回帰係数を求めたりすると,変数を入れ替えてしまったりあまり深く考えず回帰直線を求め,間違って使ってしまう事が意外にも多いです.気をつけましょう!
まとめ
今回は2つの変数から2つの回帰直線を求め,それを描画してみました.
一般に,\(x\)から\(y\)を予測する回帰直線の式を,\(y\)から\(x\)を予測する際には使えないので注意しましょう!
今回のまとめはこれだけw
次回は回帰分析で非常に重要な指標である決定係数について解説していこうと思います!
決定係数を使うことで,求めた回帰直線がそのデータにどれくらいフィットしているのかを評価することができます.論文とかでもほんとによく使う指標なんですが,ちゃんと理解できてる人は少ないと思います.きちんと体系的に学んでいきましょう!
それでは!
(追記)次回の記事書きました!