(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
データサイエンス入門:統計講座第32回です.
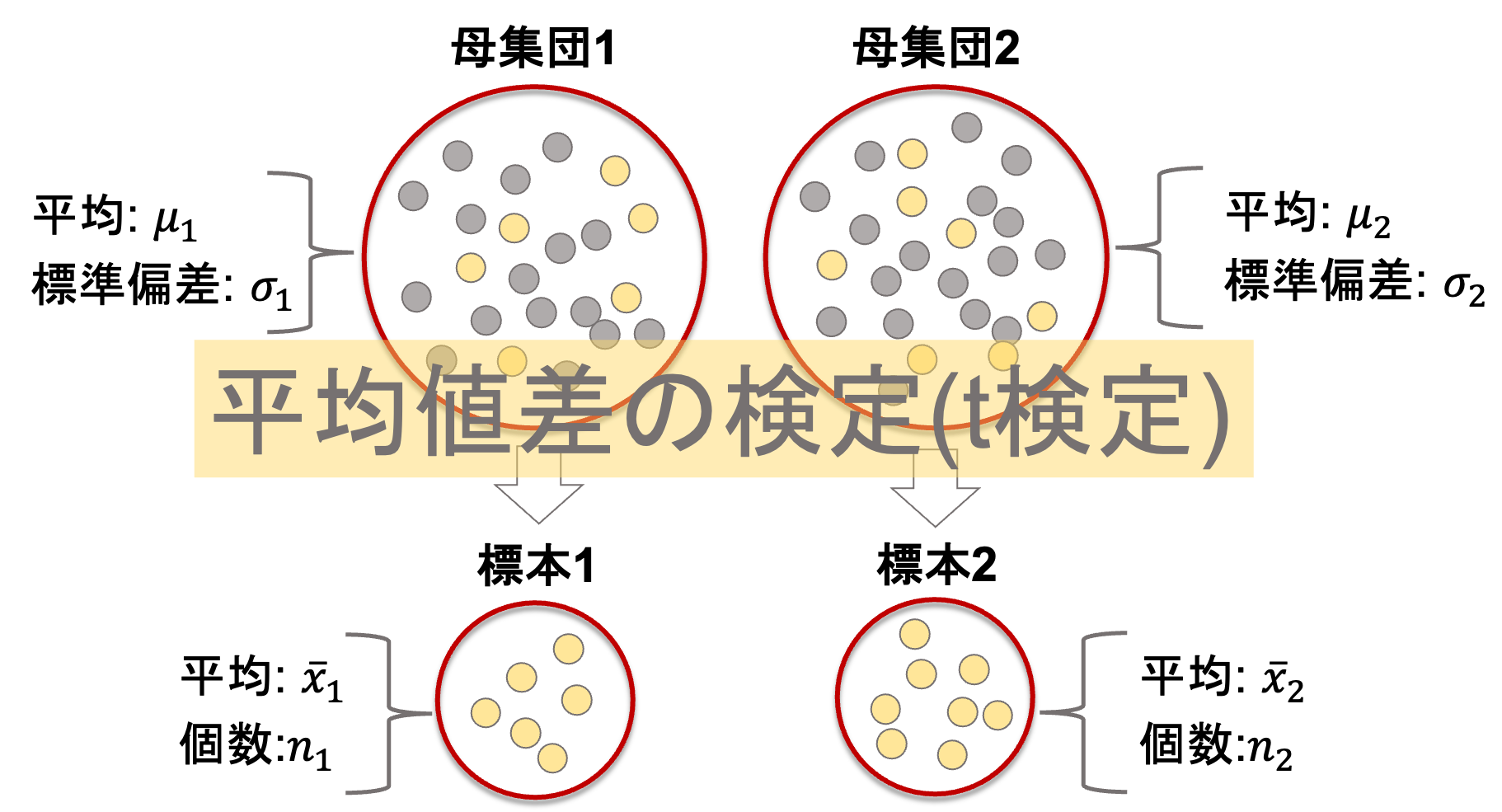
今回はついに,平均値差の検定をやります.ある2つの母集団の平均値に差があるのかを調べる検定です.
仮説検定というと,多くの人がこの「平均値差の検定」を思い浮かべるくらい有名な検定です.
現実問題でも平均値に差があるか見たいケースは多いです.例えば試薬Aと試薬Bの効果に差はあるのか,従来製品と新製品で性能の差はあるのか,パート社員と正社員の作業効率に差はあるのかなど,例はいくらでもあるでしょう.
「平均値の差を検定したいから統計学を学んでる」という人も多いかと思います.論文執筆にも最も必要とされる検定の一つです.
比率の差の検定がベースとなるので,第28回の記事が理解できれば今回の記事も簡単に理解できると思います.それではやっていきましょう!
目次
対応ありと対応なし
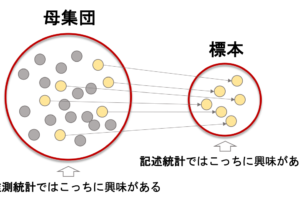
平均値差の検定をする際に,それぞれの母集団が独立なのかそうではないのかによって,少し検定の内容が変わってきます.
例えばランダムに集めた100人のグループ2つからそれぞれ平均値を計算したら,それはお互いが独立した群と言えます.逆に,100人のグループから2つの値を取るケース(例えば一人に商品A,商品Bを評価してもらうケース)は,独立とは言えません.独立である群を「対応のない群」といい,独立ではない群を「対応のある群」と呼んだりします.
対応があるほうが,同じ差があっても有意差がでやすくなるのはイメージできますね(つまり検定力が高い!).例えば同じAさんが商品Aを50点,商品Bを60点と評価するのと,Aさんが商品Aを50点,Bさんが商品Bを60点と評価するのでは,同じ差(10点)でも信用が異なります.
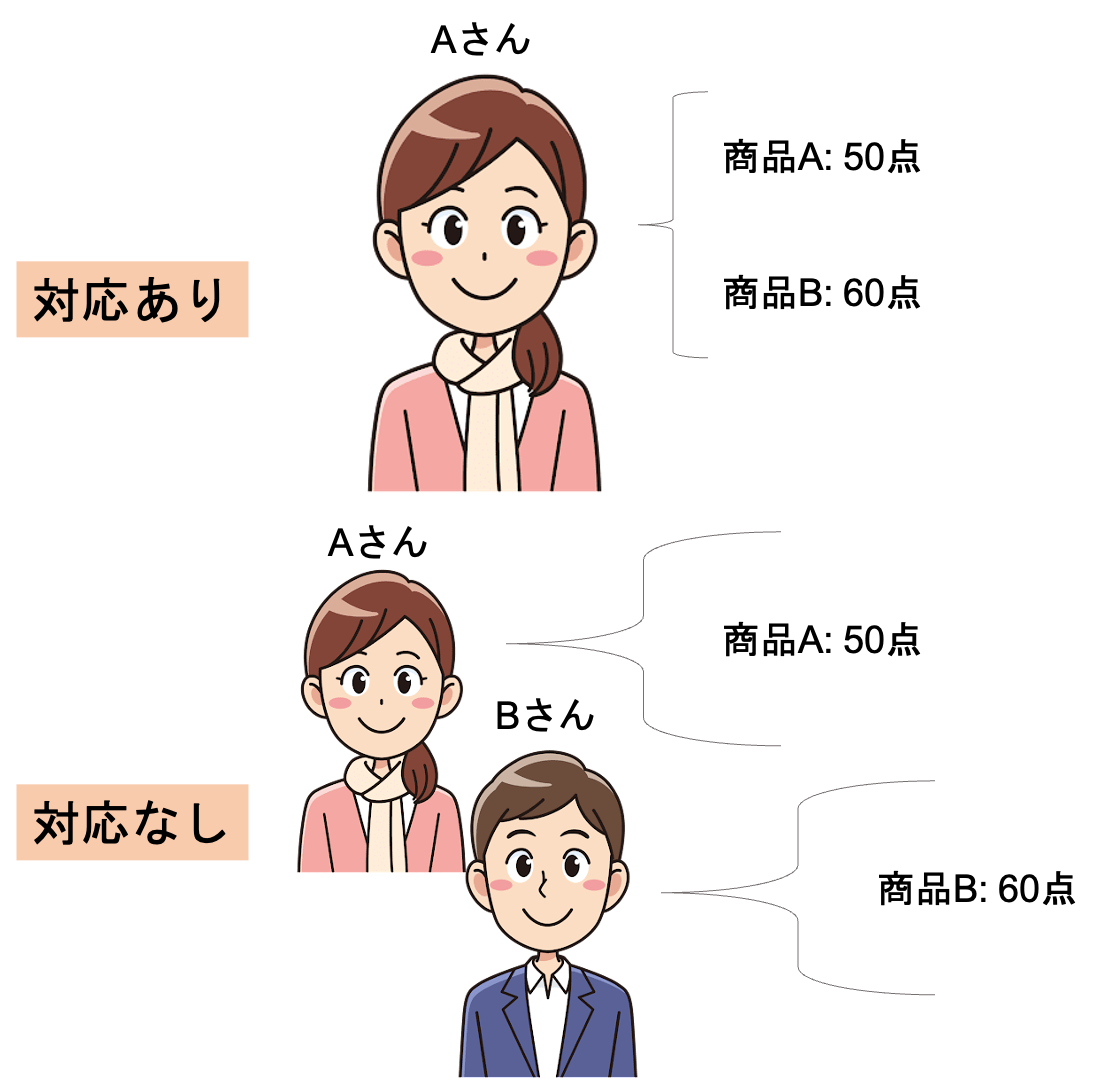
今回の記事は「対応なし」のケースを見ていきます.(現実問題でも,平均値差検定が必要となる多くのケースが対応なしのケースかと思います)
比率の差の検定は平均値の差の検定の特別なケース
第24回の比率の区間推定の時にも言及しましたが,比率というのは0と1の二値をとりうる変数の平均とも言えます.
比率の区間推定では標準正規分布を使って,平均の区間推定ではt分布を使いました.(詳しくは第24回と第25回を参照ください.また,大標本の場合は平均の区間推定も標準正規分布に近似できるんでしたね)
これと同じように,比率差の検定では標準正規分布を使っていたところを,平均値差の検定では大標本の場合は標準正規分布,小標本の場合はt分布を使います(Pythonなどの統計ツールを使う場合は,t分布を使えばOKです.これも区間推定と同じですね).
なので,比率差のことをZ検定と呼び,平気値差の検定のことをt検定(Student’s t-test)と呼びます.(大標本の場合はZ検定と呼ぶ場合もありますが,ツールなどでは大標本だろうと小標本だろうとt分布を使うので,本ブログではそこは区別せず,t検定と呼びます.)

そのとおり!そんなに難しい話ではないので,サクッと学習していきましょう!必要に応じて第28回の比率の差の検定と第25回の平均値の区間推定を参照しながら進めてください.
“平均値の差”が従う確率分布を考える(大標本の場合は標準正規分布に近似)
比率の差の検定では,標本の比率の差が従う確率分布を考え,前回の連関の検定では,観測度数と期待度数の差(\(\chi^2\))が従う確率分布を考えましたね.
平均値の差の検定では,当然”平均値の差”が従う確率分布を考えます.
次回の記事でPythonのコードを紹介する際に具体例で説明するとして,理論の説明は一般化した記号で解説していきます(流石に数式も慣れてきたと思います.不安な人は第25回を見ながら進めてくださいね!)
ある二つの母集団(平均がそれぞれ\(\mu_1, \mu_2\), 標準偏差が\(\sigma_1, \sigma_2\)とします)からそれぞれ標本(\(n_1\)個と\(n_2\)個)を取ってきて,それぞれの標本の平均を\(\bar{x}_1, \bar{x}_2\)とします.(いつも通りの記号ですよね!)
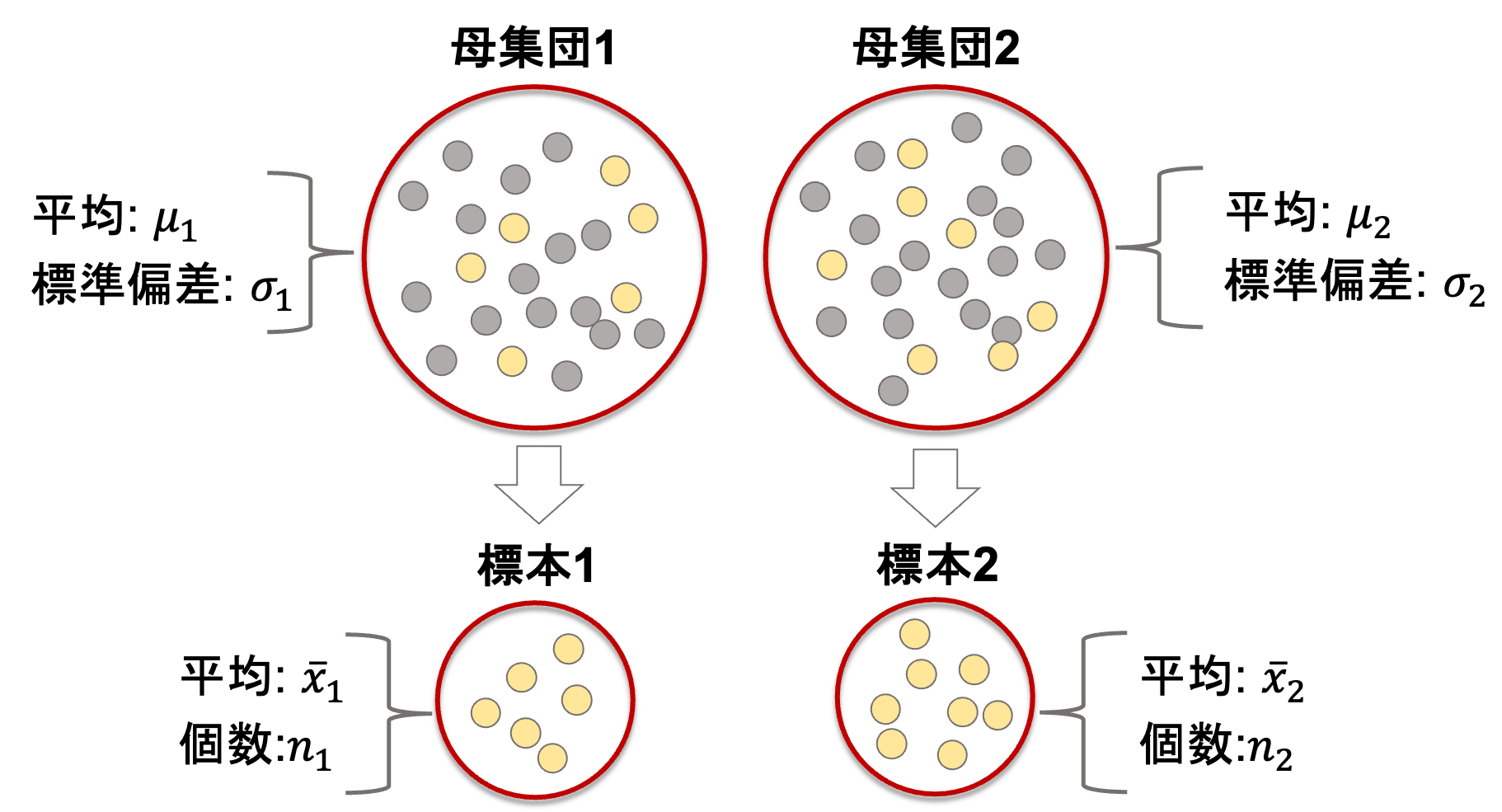
今回注目すべきは標本の平均値差\(\bar{x}_1-\bar{x}_2\)です.この統計量がどのような分布になっているのかを見ればOKですね!
先述したとおり,比率も平均と同じ考えが適用できるので,比率の差の検定同様に,標本の平均値差\(\bar{x}_1-\bar{x}_2\)の標本分布は以下に示す平均\(\mu\),分散\(\sigma^2\)の正規分布になります.
$$\mu=\mu_1 – \mu_2$$
$$\sigma^2=\frac{{\sigma_1}^2}{n_1} + \frac{{\sigma_2}^2}{n_2}$$


そのとおり!これも第25回の平均値の区間推定と同じです.(しかし\({s’}_1\)と\({s’}_2\)は,それぞれ不偏分散\({{s’}_1}^2\)および\({{s’}_2}^2\)の平方根です.不偏分散については第6回で詳しく解説しているのでそちらをご確認ください.
つまり,\(\sigma^2\)は以下のようになり,
$$\sigma^2=\frac{{{s’}_1}^2}{n_1} + \frac{{{s’}_2}^2}{n_2}$$
これを標準化(第9回参照)すれば,標準正規分布の形に持っていけます.(しかしこれは,\(n_1\)および\(n_2\)が大きい場合です.これは第25回で説明したのと同じですね.)
$$z=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\sqrt{\frac{{{s’}_1}^2}{n_1}+\frac{{{s’}_2}^2}{n_2}}}$$

この数式は別に覚えなくていいんです.(順を追っていけばそんなに難しい数式ではないんですが)
重要なのは流れです.標本のそれぞれの平均の差の確率分布が大標本であれば正規分布に近似でき,母集団の分散の代わりに各標本の不偏分散を使うというところを押さえておきましょう!(第25回の平均値の区間推定と同じですね)
平均値差の検定では,帰無仮説は当然「2つの母集団の平均に差はない(\(\mu_1=\mu_2\))」とするので,先ほどの\(z\)の式は
$$z=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{{{s’}_1}^2}{n_1}+\frac{{{s’}_2}^2}{n_2}}}$$
となり,この式に各標本から計算した値を代入して,有意水準5%で両側検定なら\(z<-1.96\)もしくは\(1.96<z\)の時に帰無仮説を棄却し,片側検定なら,下側5%であれば\(z<-1.64\)の時,上側5%であれば\(1.64<z\)の時帰無仮説を棄却します.
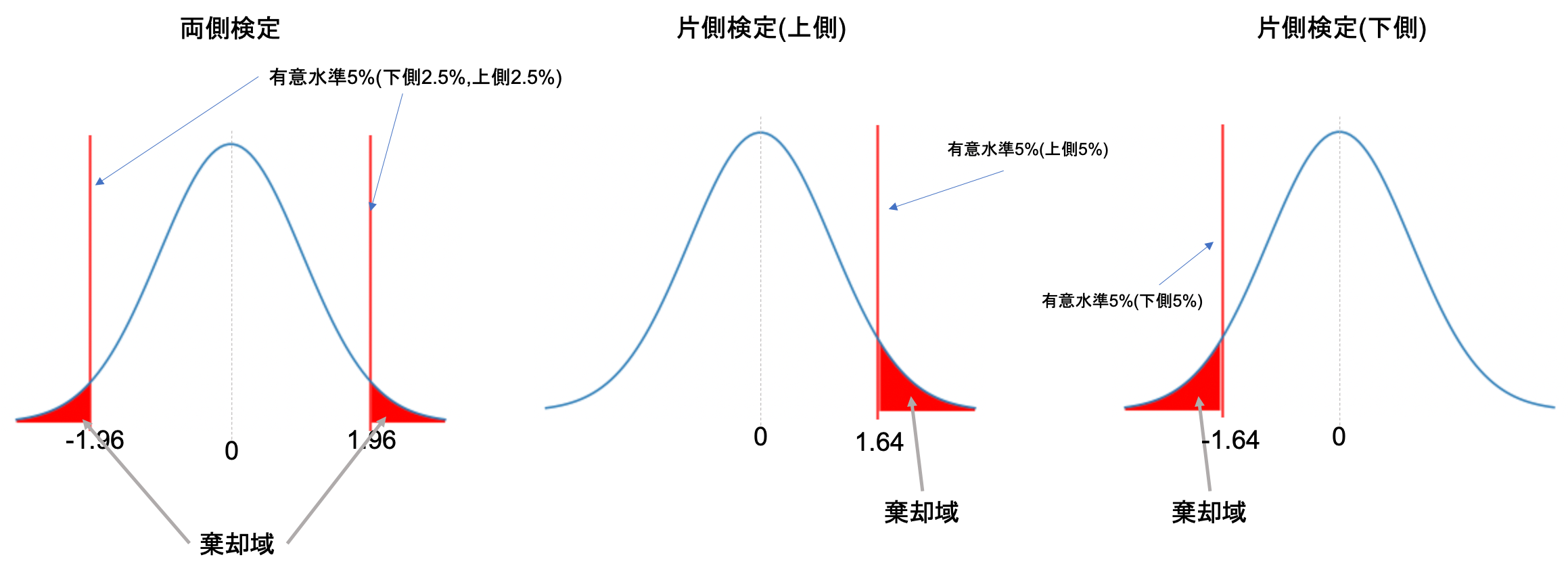
(両側検定や片側検定については,第28回を参照してください.考え方は比率の差の検定と同じです.)
小標本の場合はt分布を使う!
先述したとおり,正規分布に従うのは標本の数が大きい時です.じゃぁ小さい時はどうなるのか?
標本が小さい場合は二つの母集団が正規分布であり,かつ分散が等しい場合に限り(\({\sigma_1}^2={\sigma_2}^2\)),第26回の平均値の区間推定同様,検定統計量の分布はt分布になります.
分散が正しくない場合は別の検定(ウェルチのt検定など)を必要としますが,本講座ではそこまではやりません.通常二つの母集団の分散は当然未知の値なので,実際に等しいかはわからないのですが,たいていは等しいと仮定して検定を行います.また,二つの母集団の分散が正しいかの検定をすることができます.これについてはまた別の記事で解説します.

t分布については第26回で解説していますが,おさらいすると,平均値の区間推定において,
$$z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$$
を考える際に,母集団の標準偏差\(\sigma\)の代わりに標本の不偏分散の平方根\(s’\)を用いることによって,標準偏差よりも少し裾が長いt分布になるんでしたね.
$$t=\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}}$$
さて,それではもう一度平均値差\(\bar{x}_1-\bar{x}_2\)の標本分布を確認します.二つの母集団の分散が等しい場合(\(\sigma_1=\sigma_2\))を考えると,先述の平均値差の分布の分散\(\sigma^2\)
$$\sigma^2=\frac{{\sigma_1}^2}{n_1} + \frac{{\sigma_2}^2}{n_2}$$
は\(\sigma_1=\sigma_2\)なので
$$\sigma^2={\sigma_1}^2(\frac{1}{n_1} + \frac{1}{n_2})$$
となります.ここで,二つの母集団に共通な\({\sigma_1}^2\)の推定値をどうするか?という問題になります.
大標本の場合は\({\sigma_1}^2\)および\({\sigma_2}^2\)をそれぞれ標本の不偏分散\({{s_1}’}^2\),\({{s_2}’}^2\)を推定値として使って,その結果正規分布に近似できました.
小標本の場合は二つの母分散が等しいと仮定すると(理論上等しい必要がありますが,それは実際にはわかりません.必要であれば母分散が等しいという検定をする必要がありますが,ここではあくまでも母分散は等しいと”仮定”して進めます)二つの共通な母分散\({\sigma_1}^2\)を推定することになります.
では,\({\sigma_1}^2\)はどのように推定すればいいでしょうか?それぞれの標本の不偏分散である\({{s_1}’}^2\),\({{s_2}’}^2\)を使いますか?
今回は二つの分散は等しいことを前提にしているので,今回得られた二つの標本を一つにまとめて,その全データ(\(n_1+n_2\))における平均からの偏差の2乗和を全体の自由度で割ったものを使います.

不偏分散の計算を思い出してください(第7回参照).母集団の分散の推定量として,平均からの偏差の2乗和を自由度(n-1)で割ったものを不偏分散としていましたよね?それと同じです.
なので以下の二点を求める必要があります.
1.全データ(\(n_1+n_2\))における平均からの偏差の2乗和
2.全体の自由度
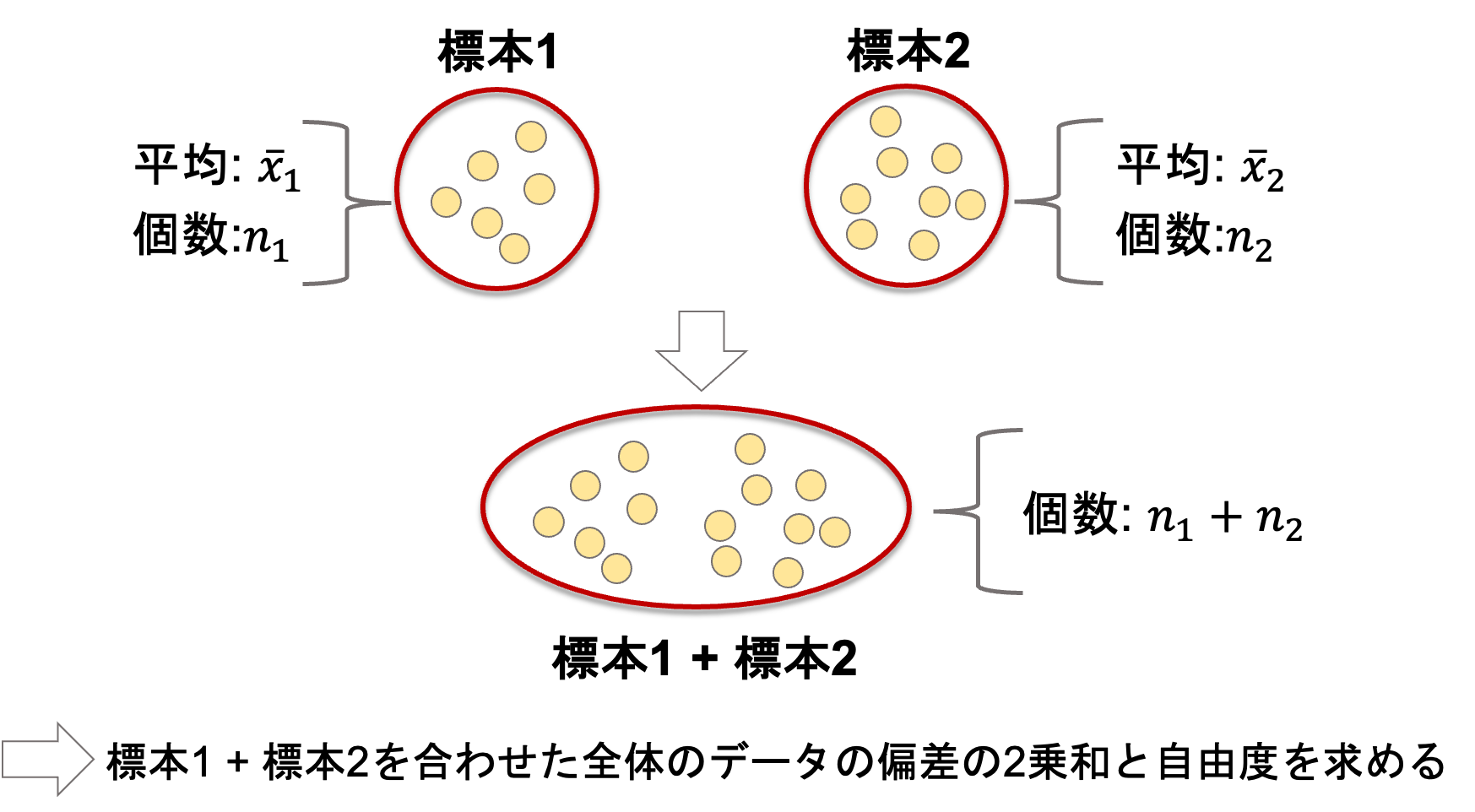
それぞれ見ていきましょう.
1.全データ(\(n_1+n_2\))における平均からの偏差の2乗和を求める
これは,数式でいうと\(\sum^{n_1}_{i=1}(x_{1i}-\bar{x}_1)^2\)と\(\sum^{n_2}_{i=1}(x_{2i}-\bar{x}_2)^2\)を足し合わせたものです.
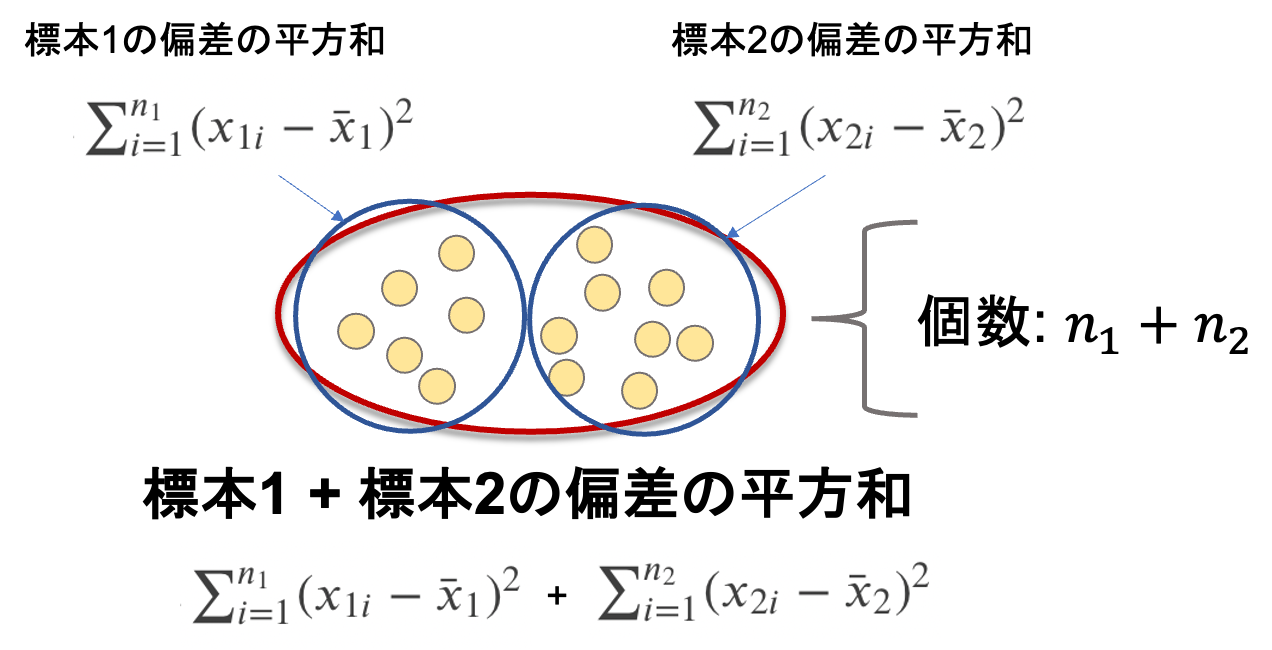
これは,\({{s’}_1}^2=\frac{1}{(n_1-1)\sum^{n_1}_{i=1}(x_{1i}-\bar{x}_1)^2}\)および\({{s’}_2}^2=\frac{1}{(n_2-1)\sum^{n_2}_{i=1}(x_{2i}-\bar{x}_2)^2}\)(第7回参照)から
\((n_1-1){{s’}_1}^2+(n_2-1){{s’}_2}^2\)となることがわかると思います.そんなに難しくないですね!
2.全体の自由度を求める
「自由度」とは文字通り「自由に値を決めれる数」です.不偏分散を求める際に,自由度「n-1」として計算をしていました.これは,\(x_1, x_2, …, x_n\)が平均\(\bar{x}\)になるためには,自由に決められる数がn-1個だからです.(例えばa, b, cの三つの値を考えた時に,平均が決められていた場合,自由に決めることができるのは,a, b, cのうち2つです.最後の一つは自動的に値が決まってしまうため)
さて,先ほどの「全データ(\(n_1+n_2\))における平均からの偏差の2乗和」の数式を見てみると,第1項が自由度\(n_1-1\), 第2項が自由度\(n_2-1\)となっています.
これは,標本1の平均が\(\bar{x_1}\),標本2の平均が\(\bar{x_2}\)と決められているので,自由に決められる数がそれぞれ\(n_1-1\),\(n_2-1\)であることからもわかると思います.
なので今回求める「全体の自由度」はこれらを足し合わせた\(n_1+n_2-2\)となります.
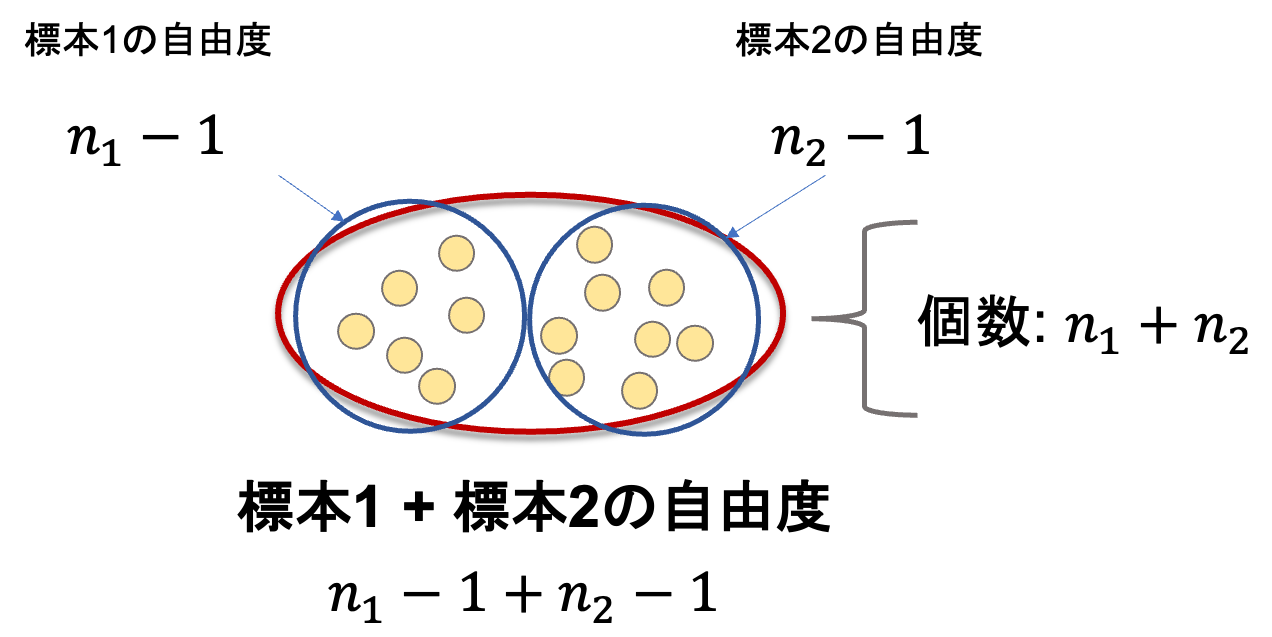
以上から,今回求めたい二つの共通な母分散\({\sigma_1}^2\)の推定値の「全データ(\(n_1+n_2\))における平均からの偏差の2乗和を全体の自由度で割ったもの」は以下の式なります.
$$\frac{(n_1-1){{s’}_1}^2+(n_2-1){{s’}_2}^2}{n_1+n_2-2}$$
これを先ほどの\(\sigma^2={\sigma_1}^2(\frac{1}{n_1} + \frac{1}{n_2})\)に代入すると
$$\hat{\sigma}^2=\frac{(n_1-1){{s’}_1}^2+(n_2-1){{s’}_2}^2}{n_1+n_2-2}(\frac{1}{n_1} + \frac{1}{n_2})$$
(\(\hat{\sigma}^2\)は\(\sigma^2\)の推定値)となり,大標本では\(z\)として計算していた検定統計量である
$$z=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\sqrt{\frac{{{s’}_1}^2}{n_1}+\frac{{{s’}_2}^2}{n_2}}}$$
は,
$$t=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\sqrt{\frac{(n_1-1){{s’}_1}^2+(n_2-1){{s’}_2}^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\frac{\bar{x}_1-\bar{x}_2-(\mu_1-\mu_2)}{\hat{\sigma}}$$
となり,これは自由度\(n_1+n_2-2\)のt分布となります.
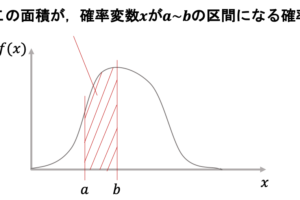
あとは今まで通り帰無仮説(\(\mu_1=\mu_2\))が正しいとした時の\(t=\frac{\bar{x}_1-\bar{x}_2}{\hat{\sigma}}\)を計算し,この値が自由度\(n_1+n_2-2\)のt分布において指定した有意水準を元に棄却域に入るかどうかを見ればいいわけです.

今回の数式は別に覚えなくてOKです.重要なのは
- 小標本の場合は,2つの母集団の分散が等しいと仮定しないとt検定はできない
- 最終的な検定統計量は自由度\(n_1+n_2-2\)のt分布に従う
というところを押さえておきましょう!
次回の記事で実際にPythonを使ってt検定をやってみます.具体例を使って実際に結果が見れるとよりイメージできると思います.
今回の記事を見て数式ばっかで何もわからなかった!という人も,是非次の記事で実際にやってみてください◎
まとめ
- 平均値差の検定には,「対応あり」と「対応なし」の二通りがある
- 比率の差の検定は,平均値差の検定の特別なケースと言える
- 大標本のとき,検定統計量は正規分布に近似する
- 小標本のとき,二つの母集団の分散が等しい場合に限り,検定統計量はt分布となる
- 平均値差の検定は,t分布を使うことからt検定とも呼ばれる.
数式は覚えなくてOKです.ただ,Step by stepにやっていけば簡単に理解できるので,是非一度は読んでみてほしいです.(完成形だけみるから嫌になるんですよね,数式って.)
次回は実際にPythonでt検定をやってみましょう!
それでは!
追記)次回の記事書きました!