線形回帰の係数の解釈の仕方(p値)【機械学習入門6】

こんにちは，米国データサイエンティストのかめ(@usdatascientist)です．

今回の記事はデータサイエンス入門の機械学習編第6回です．(講座全体の説明と目次はこちら)

追記)機械学習超入門動画講座を公開しました！動画で効率よく学習をしたい人はこちら(現在割引クーポン配布中です)

前々回と前回の記事で，正規方程式&scikit-learnを使って線形回帰のモデルを構築しました．

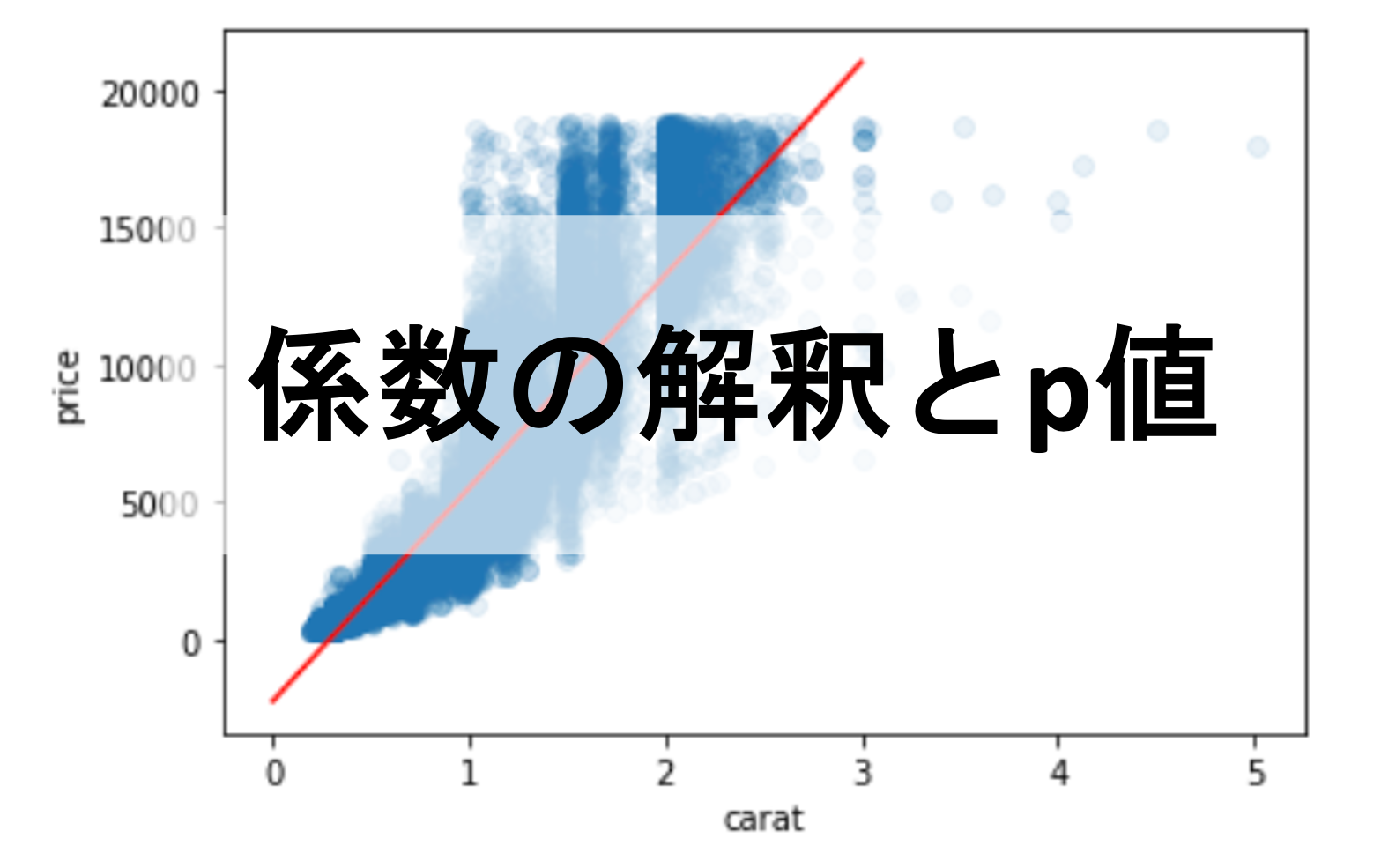
diamondsデータセットにおいて特徴量”carat”から”price”を予測するモデル$price=-2255+7755\times carat$を作りました．（シンプルにするため係数と切片の小数点は切り捨てています）

今回の記事ではこの結果についてもう少し詳しく掘り下げて解釈してみたいと思います！

係数の意味やp値を見ることで，線形回帰モデルをより理解することができ，今後のモデル構築の際にそれらの知見が生きてきます．

線形回帰の係数と切片の意味

今回の例では-2255という係数と7755という切片の数字を得ることができました．これらの数字は一体なにを意味しているのでしょうか？

1. 係数の意味

各特徴量の係数の意味は，その特徴量が1単位増えた場合に目的変数が平均的にどれくらい増えるのかを表しています．

つまり，今回の例では1カラット上がると平均的に$7755値段が上がるというわけですね．(複数特徴量がある場合は，「他の全ての特徴量が固定されたとき」という条件が入ります)

補足
“平均的に”というのは，「線形回帰は条件付き平均」という考え方から来ています．このあたりが「？？」ば方は統計学講座13回以降で詳しく解説しているので参考にしてください

2. 切片の意味

各特徴量が0だった場合の目的変数の平均値です．

今回の例では，カラットが0だった場合の平均的な価格は-$2255ということ．値段が負なので，カラットの値がある程度ないと値段がつかないってことですね！これもダイヤの値段を考える上では直感に即しているかと思います．

係数に有意差があるか

係数の値の大きさは，その特徴量の目的変数に対する影響力の大きさとも言えます．

仮に係数がとても小さかったら？

もしかしたらその特徴量は目的変数とは関係がないかもしれません．つまり線形回帰の結果の係数を見れば，その特徴量が目的変数に対して影響がないのかどうかがわかるということです！

でもどれくらい小さかったら影響がないと言えるのか？これは，統計的仮説検定で有意差を見ることによって知ることができます．

目的変数に関係がない特徴量を入れて学習しても意味がないからね！

補足
統計的仮説検定については，統計学講座第27回以降で解説してます．また，動画講座でもかなり詳しく解説しているので是非受講ください！

仮説検定では帰無仮説と対立仮説を立てるんでした．帰無仮説は$\theta_j=0$で対立仮説は$\theta_j\neq0$です．

つまり，その係数は0じゃないってことを統計的に言いたいんだね！

$\theta_j$が0より十分大きい値だったら帰無仮説を棄却できそうです．じゃぁどれくらい大きい必要があるのか？

それを見るには，ここでもやはりt分布を見ます．以下のt値が自由度$m-n-1$($m$:データ数，$n$:特徴量数)のt分布に従います．

$$t=\frac{\hat{\theta_j}-0}{SE(\hat{\theta_j})}$$

なお，$\hat{\theta_j}$は線形回帰から得られた$j$番目の特徴量の係数，$SE(\hat{\theta_j})$は$\hat{\theta_j}$の標準誤差(standard error)です

補足
機械学習の結果得られた係数$\theta_j$は，今回のような仮説検定の文脈では推測値なので$\hat{\theta_j}$のように^(ハット)をつけるのが正しいですが，一般的に真の$f(X)$は線形回帰のモデルとは限らないので他の記事では^(ハット)をつけていません．

このt値がt分布に従う証明は少し骨が折れるので割愛しますが，こちらの記事で書いていたt値の式$t=\frac{\bar{x}-\mu}{\frac{s’}{\sqrt{n}}}$と形は同じです．

標準誤差$SE$というのは，推定量の標準偏差のことです．標準偏差はばらつきを表す指標でしたね？つまり標準誤差は推定量がどれくらいばらついているのかを表す指標であり，推定の精度の指標と言えます．(ばらつきが小さい方が大きい場合よりも推定の精度が高いと言えます)

例えば母集団の平均の推定量として標本の平均を使いますが，複数の標本から標本平均計算した時の標準偏差は標準誤差と言えます．(この辺りについては統計学講座第7回で解説しています．)

補足
単に「標準誤差」というと，「標本平均の標準偏差」を指すことが多いです．

今回の$\theta_1$の標準誤差はどう求めるんだろう？

これも式を導出するのに骨が折れるのですが，簡単に紹介します(行列演算が苦手な人は飛ばしてしまってOKです．)．係数$\hat{\theta_j}$の標準誤差$SE(\hat{\theta_j})$は,分散$Var(\hat{\theta_j})$の平方根を取ればOKです．$j$という添字は行列表記で考えれば不要なのでベクトル$\theta$の形を考えます

$$SE(\hat{\theta})^2=Var(\hat{\theta})=E((\hat{\theta}-\theta)(\hat{\theta}-\theta)^T)$$

$\hat{\theta}$の分散$Var(\hat{\theta})$は上記のように表すことができます．これは，推定量の分散は「推定値と真の値の差の二乗の平均」ということからもわかるかと思います．$E()$は期待値で，平均を取っていると思ってください．(なお，$E(\hat{\theta})=\theta$であることからも，分散の式と上記の式を見比べても理解できるのではないでしょうか？)

ここで，$\hat{\theta}-\theta$について考えてみます．今回真のモデルを$f(X)=\mathbf{X}\theta+\epsilon$と仮定していることと，正規方程式より，$\hat{\theta}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$であり, $E(\epsilon)=0$なので$E(\mathbf{y})=\mathbf{X}\theta$であるので，

\begin{align}
\hat{\theta}-\theta & =\hat{\theta}-E(\hat{\theta}) \\
& = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}-(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}\theta \\
& = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{y}-\mathbf{X}\theta) \\
& = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\epsilon
\end{align}

とすると，上記の$Var(\hat{\theta})$は

\begin{align}
Var(\hat{\theta})& =E((\hat{\theta}-\theta)(\hat{\theta}-\theta)^T) \\
& = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^TE(\epsilon\epsilon^T)\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \\
& = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^TVar(\epsilon)\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}
\end{align}

となり，$Var(\epsilon)$は，誤差$\epsilon$の分散で，$\sigma^2$としておきます．すると上記の式は

$$Var(\hat{\theta})=\sigma^2(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}=\sigma^2(\mathbf{X}^T\mathbf{X})^{-1}$$

$\sigma^2$は誤差$\epsilon$の分散ですが，誤差というのは，真の$y$の値と予測値$\hat{y}$の差のことで，その誤差のばらつきがどれくらいになるのかは分かりません．これを求めるには全てのデータ(母集団)が必要だからです．

なので推定量$\hat{\sigma}^2$を，学習データ$y_1, \cdots, y_m$とその予測値$\hat{y_1}, \cdots, \hat{y_m}$の誤差を用いて計算します．

分散については統計学講座第5回の記事に解説があるので式を忘れてしまった人は参考にしてください．今回は$\sigma^2$の推定量$\hat{\sigma}^2$ということで，不偏分散の式$\frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\bar{x})^2}$を参考に以下のように$\hat{\sigma}^2$を計算します．

補足
$\sigma$を推定量$\hat{\sigma}$で代替することになるので，標準誤差$SE(\hat{\theta})$も実際には推定量ということで $\hat{SE}(\hat{\theta})$とするのが正しいですが，みにくくなってしまうので本講座ではそこまで厳密に書きません．

$$\hat{\sigma}^2=\frac{1}{m-n-1}\sum_{i=1}^{m}{(y_i-\hat{y_i})^2}$$

ただし$m$はデータ数，$n$は特徴量数です．$\hat{\sigma}$はRSE(residual standard error)と呼ばれ，誤差$\epsilon$の標準偏差の推定量です．

RSEは「モデルがどれくらいデータにフィットしていないか」を表す指標として使うことができるのがわかると思います．

誤差のバラツキが大きいってことはあまりデータにフィットしていないってことだね！

また，$\sum_{i=1}^{m}{(y_i-\hat{y_i})^2}$をRSS(residual sum of squares)ということもあります．これは誤差の二乗和であり，この平均を取ったのが第2回で紹介した損失関数にも使うMSEです．(RSSを損失関数としてもいいでしょう)

数式だらけでなにがなんだかわからない！！

ここまでの話が分からなくても大丈夫．重要なのは係数が0ではないことを統計的に言うために,上述したt値$\frac{\theta_j-0}{SE(\theta_j)}$を求めてそれが自由度$m-n-1$のt分布において棄却域に入るのかどうかをみればいいということ．(t分布を使った棄却/採択については統計学第32回あたりでやっているので参考にしてみてください．)

有意差があるかを見るには，最終的にp値を計算すればいいんでしたね(p値については統計学講座第28回で解説してます)

それでは，実際にPythonを使ってp値を計算してみましょう！

Pythonで係数のp値を計算してみる

今回も，前回までの記事で使っていたdiamondsデータセットを使ってみましょう！

import numpy as np
import seaborn as sns
from sklearn.linear_model import LinearRegression
df = sns.load_dataset('diamonds')
df = df[(df[['x','y','z']] != 0).all(axis=1)]
X = df['depth'].values
y = df['price'].values
model = LinearRegression()
X = X.reshape(-1, 1)
model.fit(X, y)
print(model.coef_, model.intercept_)

import numpy as np

import seaborn as sns

from sklearn.linear_model import LinearRegression

df = sns.load_dataset('diamonds')

df = df[(df[['x','y','z']] != 0).all(axis=1)]

X = df['depth'].values

y = df['price'].values

model = LinearRegression()

X = X.reshape(-1, 1)

model.fit(X, y)

print(model.coef_, model.intercept_)

[-29.86685265] 5775.256869212753

1	[-29.86685265] 5775.256869212753

今回は試しに”depth”を特徴量とした線形回帰を構築します．この辺りは前回の記事でやった通りですね．
学習後のモデルのパラメータをみると，”depth”に対応する係数が-29.8とでました．これはつまり，depthが1上がると値段が平均的に-$29.8減少することを意味します．
前回やった”carat”と比べると小さい値のように見えます．この係数が0ではないことを統計的に示してみましょう！

まず，準備として線形回帰のパラメータ$\theta$，切片の係数1を含めた行列$\mathbf{X}$と，各データの予測値$\hat{\mathbf{y}}$をつくります．

X_ = np.append(np.ones((len(X),1)), X, axis=1)
theta = np.append(model.intercept_,model.coef_)
y_preds = model.predict(X)

X_ = np.append(np.ones((len(X),1)), X, axis=1)

theta = np.append(model.intercept_,model.coef_)

y_preds = model.predict(X)

次に，$RSE=\hat{\sigma}=\sqrt{\frac{RSS}{m-n-1}}$と$RSS=\sum_{i=1}^{m}{(y_i-\hat{y_i})^2}$および$SE(\hat{\theta})^2=\hat{\sigma}^2(\mathbf{X}^T\mathbf{X})^{-1}=RSE^2(\mathbf{X}^T\mathbf{X})^{-1}$を計算します．

RSS = np.sum((y-y_preds)**2)
RSE = np.sqrt(RSS/(len(X_)-len(X_[0])))
SE_sq = RSE**2 * np.linalg.inv(np.dot(X_.T,X_)).diagonal()

RSS = np.sum((y-y_preds)**2)

RSE = np.sqrt(RSS/(len(X_)-len(X_[0])))

SE_sq = RSE**2 * np.linalg.inv(np.dot(X_.T,X_)).diagonal()

そして$t=\frac{\hat{\theta}-\mathbf{0}}{SE(\hat{\theta})}$を計算します．

t = theta/np.sqrt(SE_sq)
print(t)

1 2	t = theta/np.sqrt(SE_sq) print(t)

[ 7.79972831 -2.4914259 ]

1	[ 7.79972831 -2.4914259 ]

すると，各パラメター$\theta_j$に対してのt値が計算されました．今回興味がある$\theta_1$のt値は-2.49ですね．

それではこのt値の自由度$n-m-1$のt分布におけるp値を見てみましょう．p値を見るには stats モジュールを使ってt分布のCDF(累積分布関数)をみて，確率分布の面積を見ればいいんでしたね(統計学講座第33回参照)

p = [2*(1-stats.t.cdf(np.abs(t_val),(len(X_)-len(X_[0])))) for t_val in t]
print(p)

1 2	p = [2*(1-stats.t.cdf(np.abs(t_val),(len(X_)-len(X_[0])))) for t_val in t] print(p)

[6.439293542825908e-15, 0.012726132305307836]

1	[6.439293542825908e-15, 0.012726132305307836]

t値の正負の値に対応できるように絶対値を取り，全体の面積1から引いています．両側検定としたいので2を掛けています．(リスト内包表記についてはデータサイエンスのためのPython講座第4回を参照ください)

すると$\theta_1$に対してのp値が0.013だと言うことがわかりました．これは有意水準を5%とするとp<0.05なので有意差ありという結果になり，帰無仮説$\theta_1=0$を棄却することができ，対立仮説$\theta_1\neq0$を成立させることができます．

つまり，特徴量depthはpriceと関係があるということが結論付けれるわけです．

試しにdepthとpriceのscatterplotを見てみましょう

sns.scatterplot(x=df['depth'], y=df['price'], alpha=0.1)

1	sns.scatterplot(x=df['depth'], y=df['price'], alpha=0.1)

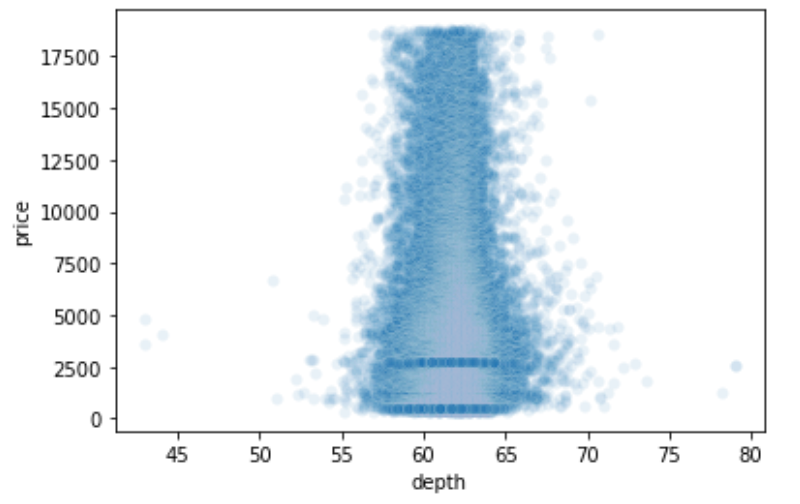
んー，これもなかなかカオスですね．とてもdepthとpriceが線形モデルに置き換えたとして関係があるようには見えませんが，p値を見ると有意差が出ています．

これはなぜでしょうか？

これはサンプル数が多すぎたために，検定力が高くなり有意差が出やすくなってしまっていることが原因です．検定力については統計学講座第30回や統計学動画講座で詳しく解説しています．

特に機械学習の文脈では大量の学習データを使って学習することが多く，精度向上のためにそれが良しとされています．そのため，機械学習のモデルのパラメータに対して統計を使った仮説検定を行うと，検定力が高くなりすぎて求めたp値があまり意味のないものになりかねないと言う点は注意してください．

じゃぁこのp値はどう扱えばいいの？

通常，複数の特徴量を使ってモデル構築をした際に特徴量を選択する際にp値を参考にすることがあります．(例えば最もp値が大きい特徴量をモデルから排除するなど．この辺りは今後の記事で扱います．)

特徴量なんて使えるものは全部使えばいいんじゃないの？

そう言うわけにもいかない場合が多いんです．この辺りについては別の記事で詳しく解説しますが，特徴量が多すぎると起きる問題がいくつかあります．第4回の正規方程式の記事でも，特徴量数がデータ数を上回ると解がでないのも問題の一つですね．他にも色々と特徴量を減らさないといけない場面があるんです．

係数のp値を求める方法はわかったけど，数式もよく分からないしましてやこれをいちいち実装して求めるのは無理だよ！

それはその通りですね笑．実はこれらのp値や他の情報を一発で求める方法があります．実際の業務では自分でスクラッチで求めるのではなくて，ライブラリを使って簡単に求めればOKです．

補足
得られた情報をきちんと理解して処理するためにも，一度自分で実装してみるといいです．今回は練習だと思って是非自分でコードを書いて，ライブラリの結果と一致することを確認しましょう！

statsmodelsを使って一発でp値を確認する

scikit-learnではp値などの情報を確認する術はありません．scikit-learnはあくまでも”高精度なモデルを構築する文脈での機械学習”に特化したライブラリだと思ってください．今回のようなp値を求めるのはどちらかというと統計学の分野なので， statsmodels を使います．

statsmodels はPythonで統計処理を行う際に利用するモジュールで， stats モジュールの補助的なモジュールでした．(統計学講座第28回などにも出てきていますね)

statsmodels.api というモジュールにある OLS というクラスを使います．OLSはOrdinary Least Squaresの略で，最小二乗法を使った線形回帰だと思ってください．

import statsmodels.api as sma
X2 = sma.add_constant(X)
est = sma.OLS(y, X2)
est_trained = est.fit()
print(est_trained.summary())

import statsmodels.api as sma

X2 = sma.add_constant(X)

est = sma.OLS(y, X2)

est_trained = est.fit()

print(est_trained.summary())

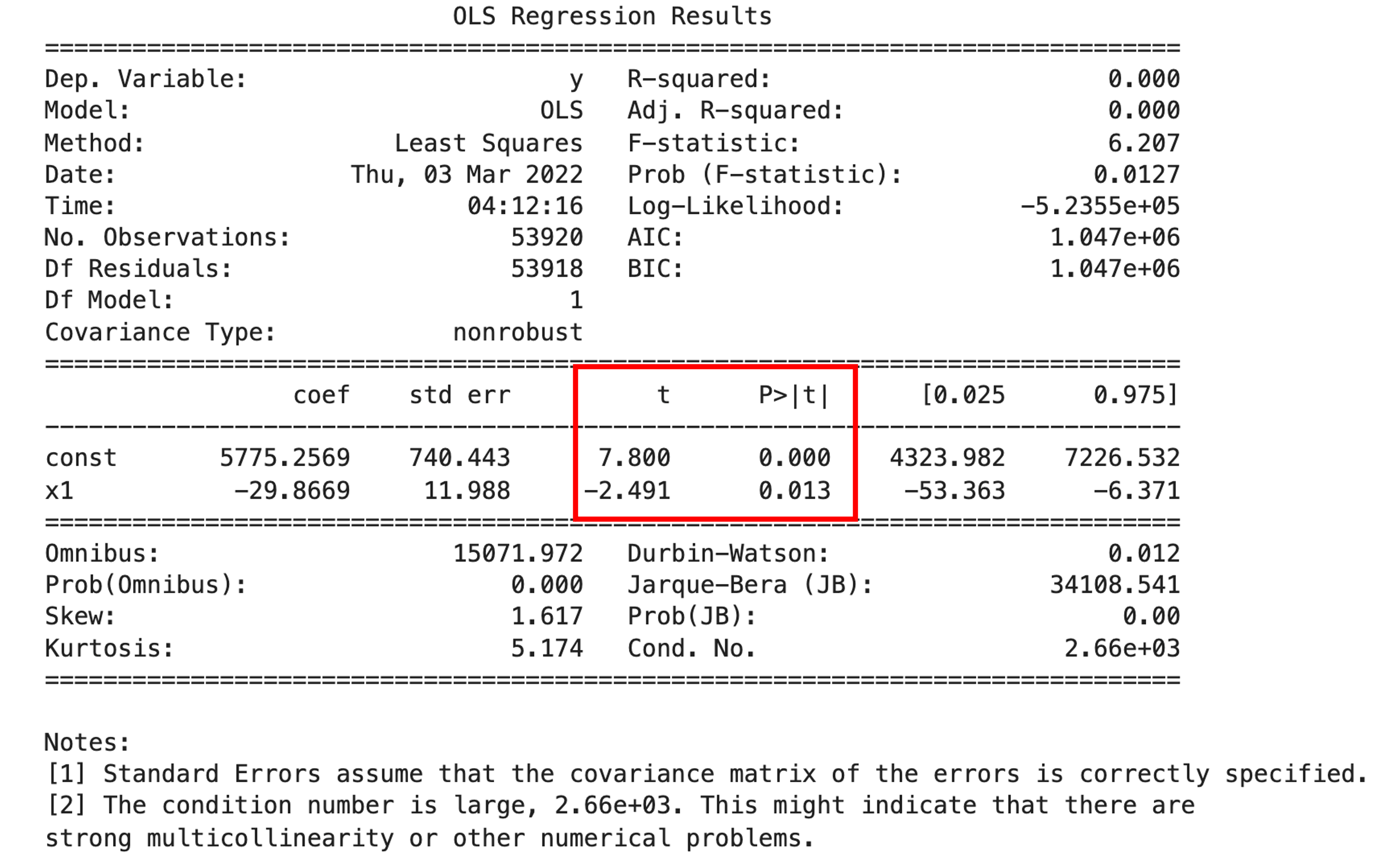
このように簡単に必要な情報にアクセスすることができます．t値とp値が先ほど求めたものと同じであることを確認しましょう！

以下のように複数の特徴量を使ってそれぞれのp値を見ることもできます．

import statsmodels.api as sma
X = df[['carat', 'depth', 'table', 'x', 'y', 'z']].values
X2 = sma.add_constant(X)
est = sma.OLS(y, X2)
est_trained = est.fit()
print(est_trained.summary())

import statsmodels.api as sma

X = df[['carat', 'depth', 'table', 'x', 'y', 'z']].values

X2 = sma.add_constant(X)

est = sma.OLS(y, X2)

est_trained = est.fit()

print(est_trained.summary())

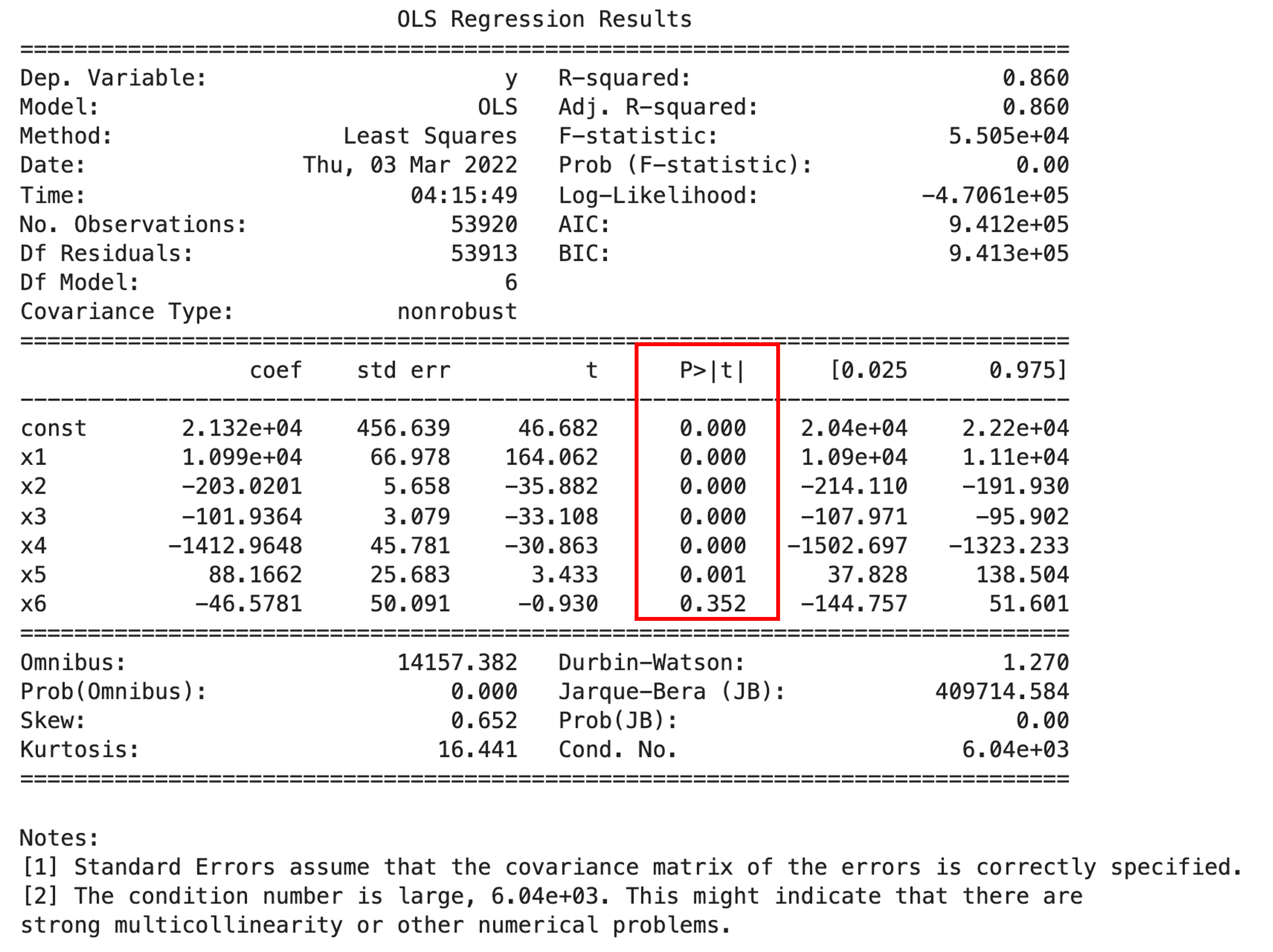
連続値の特徴量を全て特徴量にしてみました．すると最後の特徴量$X_6$の係数$\theta_6$のp値が0.352と，有意差なし(p>0.05)と言う結果になっています．つまり特徴量”z”は”price”の予測には不要であり，モデルから落としてもいいという判断ができるわけです．

この辺りの特徴量選択についてはまた別の記事で詳しく解説します．

今回はひとまず，このようにそれぞれの係数が0ではないかどうか(有意差があるかどうか)を計算してp値で判定することができるということを抑えておきましょう！

補足
“depth”単体でモデルを構築したときのp値と，他の特徴量を含めた際の”depth”のp値が異なっているのがわかると思います．これは，ある特徴量単体でモデルを作った時に有意差が出なかったとしても，他の特徴量を含めると有意差が出て，モデル構築に有効になることがあるということを意味しています．この辺りも今後の記事で扱う予定です

補足
カテゴリ変数(diamondsデータセットでいうと”cut”や”color”)も特徴量として使うことができます．少し工夫が必要なんですが，そのやり方については．今後の記事で紹介していきます！

まとめ

今回も長くなってしまいましたが，線形回帰の結果の解釈の仕方が少しはわかってきたのではないでしょうか？

今後の記事でもこのp値を使ってできることを紹介していく予定です！ただモデルを構築するのではなくて，学習したモデルの結果をより深く理解できることでできることが格段と広がります．特に線形回帰は解釈しやすいモデルなので，そこから得られる知見はかなり多いです．是非今後の学習でも，ただ闇雲にモデル構築するのではなくて，そのモデルの結果をどう解釈できるのかを考えながら学習を進めてください！