(追記)全16時間の統計学動画講座を公開しました!☆4.8の超高評価をいただいている講座です.こちらの記事に講座の内容とクーポン情報を書いていますので是非チェックしてください.
本講座も前回から仮説検定の分野に入ってきました.
仮説検定は統計学の理論の中でも最も重要な分野の一つです. 今回の記事から実際にPythonを使ってStep by Stepに検定のやり方を見ていきましょう!
是非実際に手を動かしながらやってみてください.Pythonの環境構築はこちらの記事を参考にしてみてください.
統計学を学習する最良の方法は,自分で実際にコードを書きながらデータ分析をすることです.これ以上の方法はないでしょう.
目次
実際に比率の差の検定をしてみよう!
前回の記事の例をとって,実際に比率に差があるのかを検定してみたいと思います!
数式が出てきますが,少し考えればどれも簡単に理解できるものばかりです!数式に慣れていなくても,数式だからと言って逃げずに是非一つ一つ追ってみてください.数式が読めるようになると,日本語を読むよりも統計学を簡単に理解できるようになります.
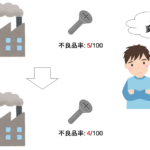
さて,前回の「工場で生産する製品の不良率」を考えてみましょう.
ある工場で製品を生産しています.不良品が生産される率を下げるため,生産過程に変更を施しました.
今回の生産過程の変更によって,ちゃんと不良品率が下がったのかを確認するため,試しに工場の一部だけ生産過程を変更し,変更前と変更後の製品をそれぞれ100個ずつ取ってきて,不良品の数を調べたとします.
不良品の数を調べたところ,変更前では不良品が5つ,変更後では不良品が4つでした.
今回とってきた計200個の製品をみるに,変更後の方が不良品の数が少なくて良さそうなんですが,この結果だけをみて「よし,生産過程を変更させよう!」と決めていいのかわかりません.
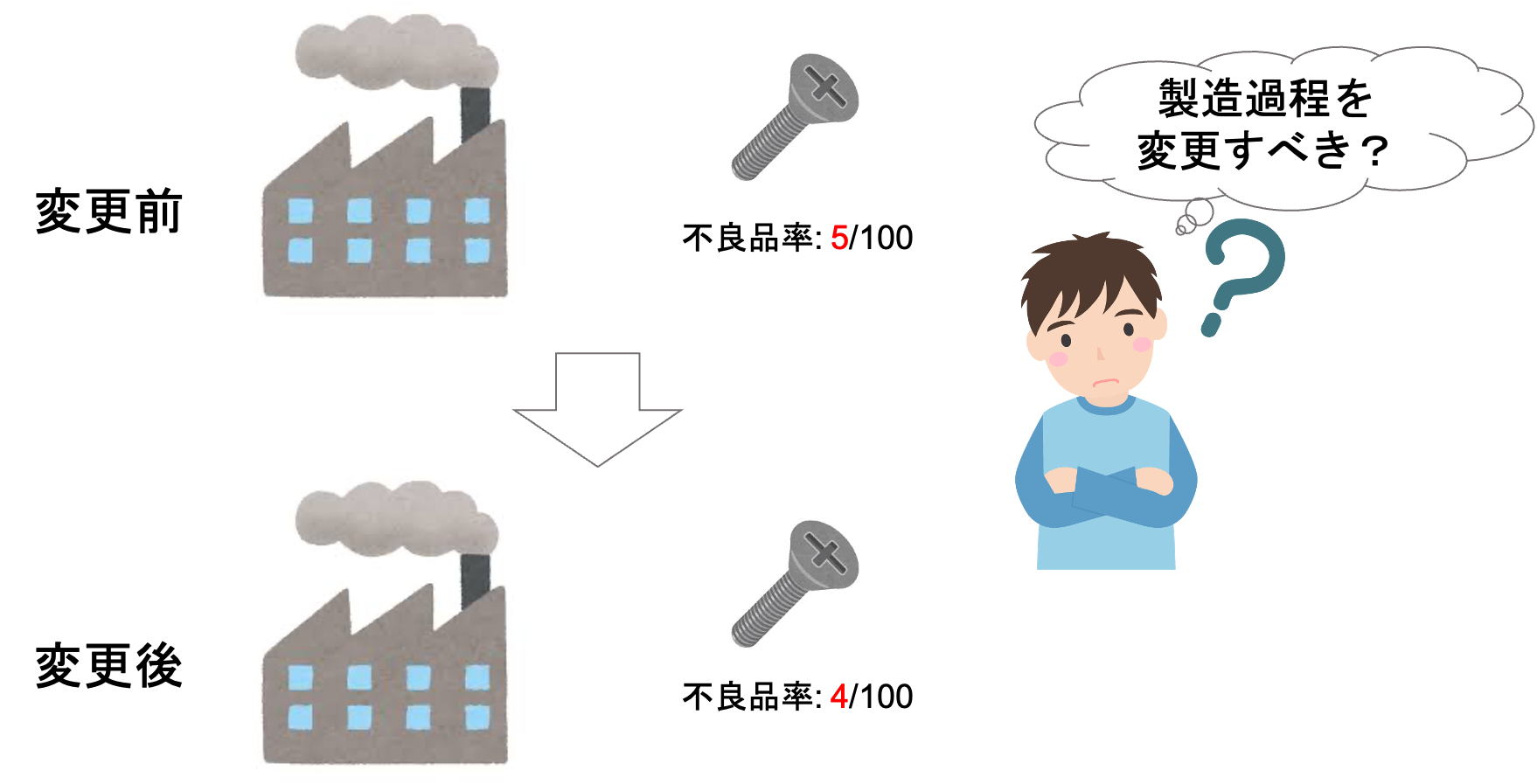
そこで使えるのが仮説検定でした.今回の変更によって”統計的に”不良品率が下がったと言えれば良さそうです.
前回の記事で解説した通り,以下の手順でやっていきましょう!
1.帰無仮説と対立仮説を立てる
2.帰無仮説のもとで標本観察を行う(標本統計量を計算する)
3.標本観察の結果,帰無仮説を棄却できるかどうかを確認する(棄却した場合,対立仮説が成立する)
1.帰無仮説と対立仮説を立てる
前回の記事で解説したとおり,帰無仮説は「たぶん間違ってるだろうなぁ」という仮説を立てるんでした.一方対立仮説は,実際に正しいと思う仮説を立てます.
帰無仮説は検定の作業を通して棄却(否定)することをねらって立てます.
前回同様今回も帰無仮説は「生産過程の変更前後で不良品率は変わらない」という仮説を立てましょう.
「差がある」というのは,無限にケースが考えられるため,「差がある」ことを言うためには「”差がない”ことを否定する」のが基本になります. そのため,差の検定では「差がない」というのを帰無仮説に設定します
では対立仮説はどうなるでしょうか?対立仮説は帰無仮説が棄却されたときに成立する仮説です.(前回記事参照)
では,対立仮説は「生産過程の変更前後で不良品率は変わる」とするのがいいのでしょうか.
この場合,二つのケースが考えられます.
- 変更前の不良品率 > 変更後の不良品率
- 変更前の不良品率 < 変更後の不良品率
今回期待しているのは1.ですよね.(変更したことによって不良品率が低くなって欲しいわけです.)
でも,対立仮説を単純に「生産過程の変更前後で不良品率は変わる」と設定すると,上述した2.のケースでも成立してしまいます.

実は,検定には片側検定と呼ばれるものと,両側検定と呼ばれるものがあります.
先ほどの1.と2.のケースの両方とも考慮して帰無仮説を棄却する検定を両側検定といい,片方のケースだけを考慮して帰無仮説を棄却する検定を片側検定と言います.
つまり,「変更後の不良品率は,変更前の不良品率より低い」という片方のケースだけの対立仮説を設定することができます.
本記事の後半で,実際に片側検定と両側検定でどのような違いがあるのかを説明します.後に出てくる図を見ると,”片側”,”両側”の意味もわかってくると思います.
2.帰無仮説のもとで標本観察を行う(標本統計量を計算する)
今回の標本は変更前・変更後の製品をそれぞれ100個取ってきて,不良品率がそれぞれ5/100(0.05)と4/100(0.04)です.
仮に変更前の製品の標本の大きさと不良品の数を\(n_1\), \(x_1\),変更後の製品の標本の大きさと不良品の数を\(n_2\), \(x_2\)とすると\(n_1=100,x_1=5,n_2=100,x_2=4\)となります.
変更前の製品の真の不良品率を\(p_1\),変更後の製品の真の不良品率を\(p_2\)とすると
帰無仮説は\(p_1=p_2\),対立仮説は\(p_1>p_2\)です.
では,今回考える標本統計量はなんでしょう?
今回は比率の差の検定なので,
$$\frac{x_1}{n_1}-\frac{x_2}{n_2}$$
がどのような標本分布をとるのかを考えます.(“標本分布”については第18回を参照してください.)
いきなり比率の差である\(\frac{x_1}{n_1}-\frac{x_2}{n_2}\)の標本分布を考えようとしても,お手上げですよね?(そんなのやったことないですもん!)
ここで,それぞれの比率の標本分布はどうなるでしょうか?これならわかりますよね?第24回でやりました.比率の標本分布は,二項分布(第19回)を考えればよく,標本サイズが大きければ,比率の標本分布は平均\(p\),分散\(\frac{p(1-p)}{n}\)(ただし\(p\)は母集団の比率)の正規分布になるんでしたね.
つまり,それぞれの母集団の比率を\(p_1\),\(p_2\)とした場合,
\(\frac{x_1}{n_1}\)の標本分布は平均\(p_1\),分散\(\frac{p_1(1-p_1)}{n_1}\)の正規分布に従い
\(\frac{x_2}{n_2}\)の標本分布は平均\(p_2\),分散\(\frac{p_2(1-p_2)}{n_2}\)の正規分布に従います.
では,比率の差である\(\frac{x_1}{n_1}-\frac{x_2}{n_2}\)の標本分布はどのような確率分布に従うのでしょうか?
実は,ふたつの確率変数(つまり今回だったら,\(\frac{x_1}{n_1}\)および\(\frac{x_2}{n_2}\))の差の平均値は,それぞれの確率変数の平均の差に等しいことがわかっています.
これは,イメージできると思います.例えば2つのサイコロの目の差の平均は?と聞かれたら,一つ目のサイコロの目の平均3.5と二つ目のサイコロの目の平均3.5を引いた数(=0)になります.
また,独立な二つの確率変数の差の分散は,それぞれの分散の和に等しくなります(!??)

これもイメージで考えましょう.
サイコロを二つ振って出た目の差のばらつきはどうなるでしょうか?一つのサイコロであれば,0~6ですよね,しかし,二つのサイコロの差がとりうる値は-5~5になります.
感覚からも正しいことがわかると思います.例えば一つのサイコロの出る目を固定して考えてみてください.一つ目が0のときの分散,1のときの分散, etc.. 独立であれば二つの確率変数の分散を足した分散が,差の分散であることが直感的に理解できます.
今回,生産過程の変更前と変更後の不良品率は独立の関係にあるので,比率の差(\(\frac{x_1}{n_1}-\frac{x_2}{n_2}\))の標本分布の平均\(\mu\)および分散\(\sigma^2\)は
$$\mu=p_1-p_2$$
$$\sigma^2=\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}$$
となります.(平均はそれぞれの母集団の比率の差,分散はそれぞれの母集団の分散の和です)

その通り!今回の帰無仮説は,「変更前と変更後の母集団の比率は変わらない」としているので,\(p=p_1=p_2\)として先の標本分布の式を書き換えてみると
$$\mu=p_1-p_2=0$$
$$\sigma^2=\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}=p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})$$
となります.

別に数式は覚えなくてOK! 重要なのは流れです.
3.標本観察の結果,帰無仮説を棄却できるかどうかを確認する(棄却した場合,対立仮説が成立する)
先述の平均\(\mu\)と分散\(\sigma^2\)の正規分布が比率の差(\(\frac{x_1}{n_1}-\frac{x_2}{n_2}\))の標本分布になるので,この正規分布において今回得られた値(変更前と変更後の差(100個中5個が不良品-変更後の100個中4個が不良品))がどれくらいの確率で起こるのかを考えればOKです.
今回は有意水準を5%として,今回得られた値が5%未満でしか起こらないなら,有意であるとして帰無仮説を棄却します.(有意水準については前回の記事を参照)
正規分布のままだと,扱いにくいのでこれを標準化した\(z\)で考えましょう.
これは区間推定の時と同じですね!(標準化については第9回を参照してください.標準化は平均\(\mu\)を引いて標準偏差\(\sigma\)で割るんでしたね)
$$z=\frac{\frac{x_1}{n_1}-\frac{x_2}{n_2}}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}}$$
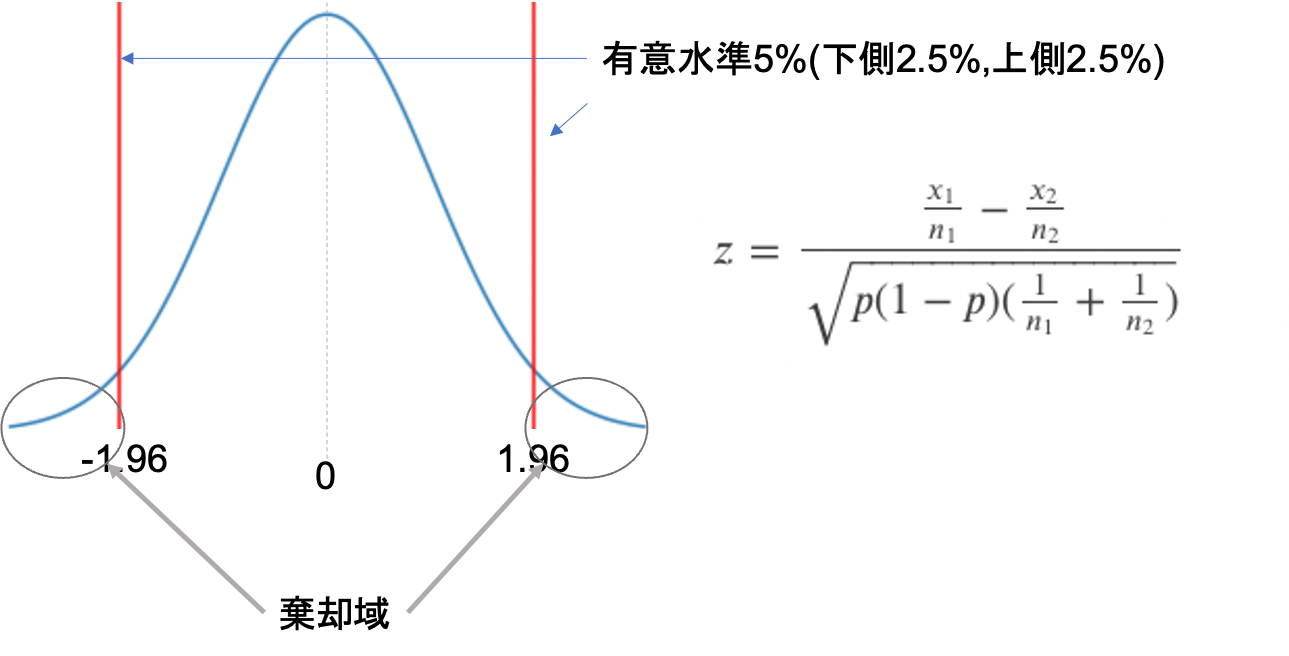
この\(z\)は,標準正規分布(平均1,分散0の正規分布)となります.両側検定で有意水準5%を取ると,\(z<-1.96\)もしくは\(1.96<z\)の時帰無仮説を棄却すればいいんですが,
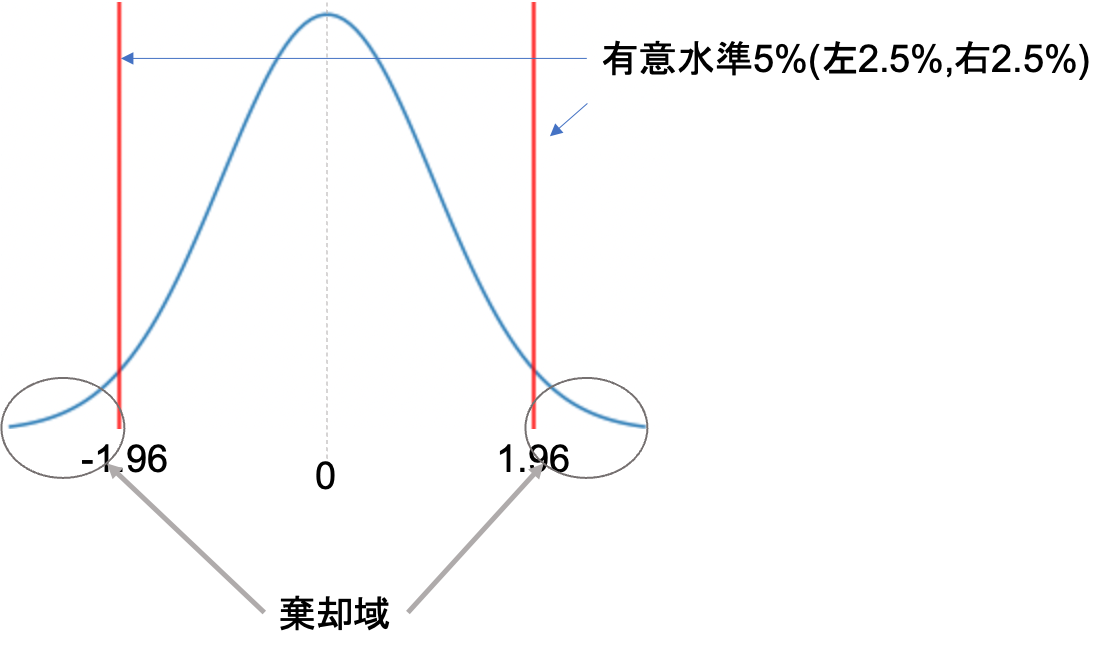
今回の対立仮説は\(p_1>p_2\)でした.この場合片側検定となり,有意水準5%とすると,両側に2.5%, 2.5%の棄却域を設けるのではなく,片側だけに5%の棄却域を設けることになります.
今回は\(p_1-p_2\)を考えているので,\(p_2\)の方が\(p_1\)よりも小さいとすると正の値(図でいうと右側)に振れることになります.なので今回は,右側に有意水準5%を設ければOKです.
正規分布において,片側5%の値は1.64です.この数字も余裕があれば覚えておくといいかもしれません◎
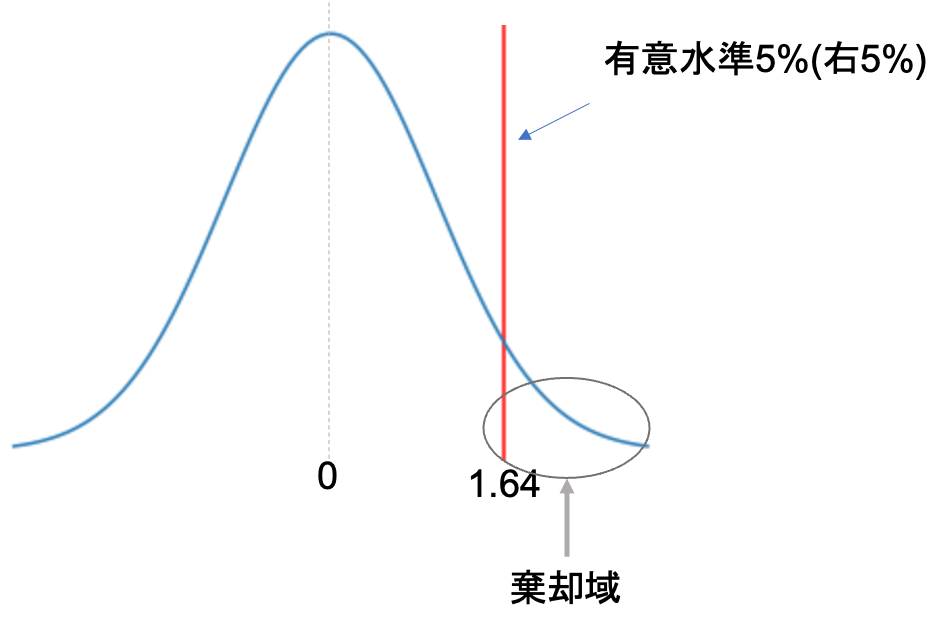
わかりやすく「右側」「左側」と書きましたが,統計学では「上側」「下側」と表現することが多いです.本講座でも今後は「上側」「下側」と表記します.
つまり,先ほどの\(z\)の値が1.64よりも大きければ「変更前より変更後の方が不良品率が低い」とし,帰無仮説を棄却し,対立仮説を成立させることができます.
それでは実際に計算してみたいんですが,,,
先ほどの\(z\)の式には母集団の比率である\(p\)が入っていますね.これは当然未知の値なので標本の値で代入する必要があります.
\(p\)の推定値として,今回の標本計200個のうち計9個が不良品だったので,9/200を代入すればOKです.数式でいうと以下のようになります.
$$\hat{p}=\frac{x_1+x_2}{n_1+n_2}=\frac{5+4}{100+100}=0.045$$
これと\(x_1=5\),\(x_2=4\),\(n_1=100\),\(n_2=100\)を\(z\)の式に代入して計算すると
$$z=\frac{\frac{x_1}{n_1}-\frac{x_2}{n_2}}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}}=\frac{0.05-0.04}{\sqrt{0.045(1-0.045)(\frac{1}{100}+\frac{1}{100})}}=0.341$$
となり,棄却域は\(z>1.64\)であることから,今回の帰無仮説は棄却できず,「生産過程の変更によって,不良品率が下がったとは言えない」結果になりました.
つまり,今回の標本で得た「不良品の数の差」は「たまたまだった」ことを否定できないわけですね.(意味のある理由とは言えない.有意ではない.ということになります.)
Pythonで比率の差の検定をやってみよう!
区間推定同様,仮説検定も流れが重要です.どの様に帰無仮説と対立仮説を立てて,なんの標本分布を確認し,有意水準はなんなのか,,,
そういったところを押さえておけば,前述した式を覚える必要はなく,実務では統計ツールで答えを出せばOKです.きちんと理論を理解した上で,ツールを使いましょう!
本講座は「Pythonで学ぶシリーズ」なので今まで同様Pythonを使って先ほどの比率の検定をしてみたいと思います.
今回はstatsmodelsというモジュールを使います.statsmodelsはstatsモジュール同様,Pythonで記述統計や推測統計をするためのモジュールで,statsに無い検定などをstatsmodelsを使って補完することができます.
statsmodelsはAnacondaの一部なので,「データサイエンスのためのPython講座」の第一回で環境構築した人はもうすでに入っています.(そうじゃない人は pip install statsmodels でインストールすればOKです.pipの使い方やモジュールについてのことなどは全てPython入門動画講座にて詳しく解説しています.Python全般の学習をしたい方は是非受講ください.)
比率の差の検定は,実は今後説明するカイ二乗検定の特別なケースだと言えます(今後講座で扱います). なので,statsモジュールにあるカイ二乗検定ができる chi2_contingency というメソッドを使って比率の差の検定をすることができるんですが,色々と使いにくいのと,まだカイ二乗検定を解説していないので今回は簡単に実行できるstatsmodelsモジュールを使います
statsmodels.stats.proption.propotions_ztest()を使って比率の差の検定をすることができます.(比率の差の検定にはZ得点(標準正規分布)を使うので,Z検定(Z-test)とも呼ばれます.)
使い方は超簡単!以下の引数を渡せばOKです.
- count : 各標本のうち,興味のある現象が起きた個(回)数 .つまり,今回なら不良品の数をリストで[5, 4]として渡す
- nobs (number of observations): それぞれの標本の数.つまり今回なら[100, 100].
- alternative : 両側検定なら‘two-sided’, 片側検定なら‘smaller’か‘larger’.smallerの場合は\(p_1<p_2\)で,largerの場合は\(p_1>p_2\).(ただし\(p_1\)は count 引数, nobs 引数の一つ目の要素に指定した標本の比率,\(p_2\)は二つ目).つまり今回は’larger'(\(p_1>p_2\))でOK.
|
1 2 |
from statsmodels.stats.proportion import proportions_ztest proportions_ztest([5, 4], [100, 100], alternative='larger') |
|
1 |
(0.34109634006443396, 0.3665155281999629) |
【超重要】p値とは?
p値とは,簡単にいうと「帰無仮説が成立するという仮定のもとで今回の標本観察の結果が起こりうる確率」です.
先の例で\(z\)の値が約0.34とでました.この0.34という数字は,どれくらいの確率で起こりうるのでしょうか?
\(z=1.64\)が5%の境目とし,それ以上の場合は上側5%の棄却域となり,帰無仮説を棄却できるんでしたね.では,\(z=0.34\)が5%よりも大きい確率で起こりうることはわかったものの,どれくらいの確率なんでしょうか?これに答えるのがp値です.
今回の結果をみると0.3665155281999629とあるので,「帰無仮説が正しいと仮定しても約37%の確率で今回のケースは起こりうるよ!」ってことです.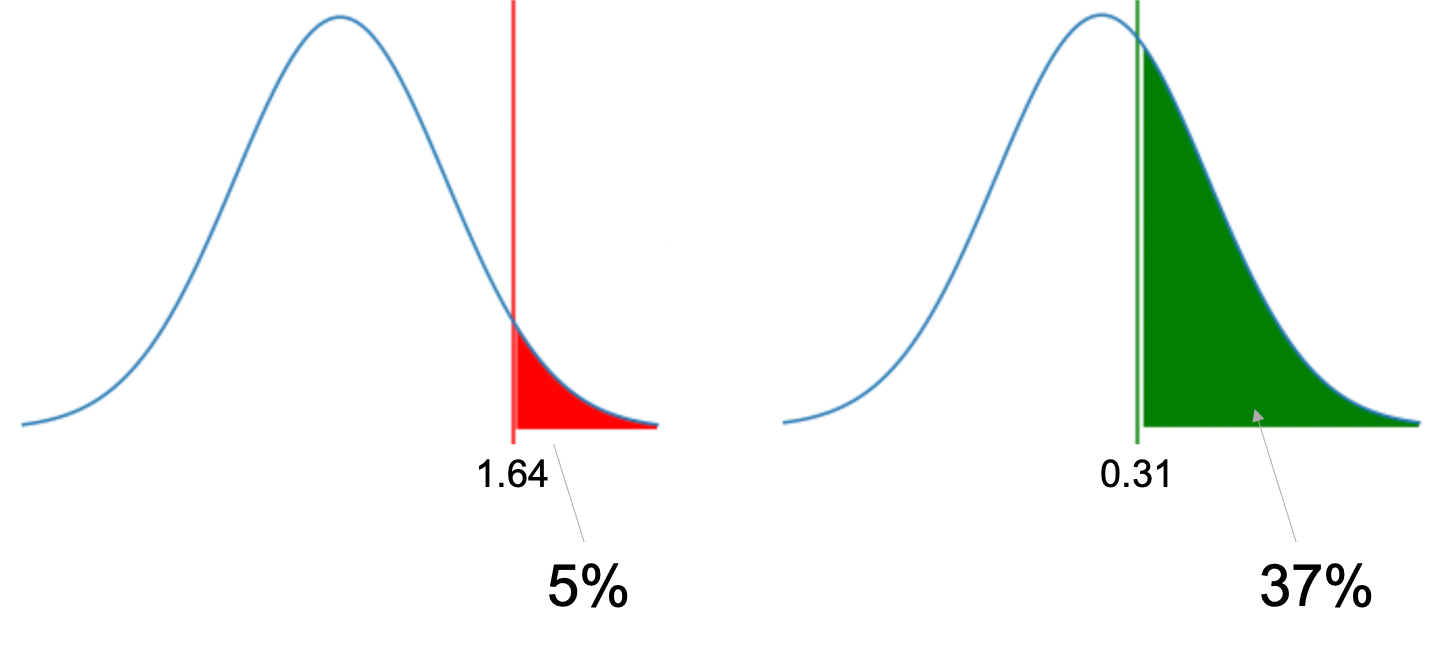
つまり,p>0.05のため,今回は棄却できないということ.
この様にツールを使って検定をすると,どの値が有意水準なのかってわからないですからね.(今回でいうと「\(z\)の値が1.64以下ならOK!」としてましたが,「1.64」という数字を覚えるのは大変です.) p値さえ出してくれればそれでいいわけです.
実際のp値の使い方としては,例えば「p<0.05で〇〇と△△に差があった」とか何かの結論の後ろに「(p<0.05)」のように添えたりします.もし学術論文などで使う場合は,そのジャーナルや学会の指示に従えばOKです.
「帰無仮説が棄却できなかった=帰無仮説が成立する」と言えるのか?
言えません.これはよくある間違いなので注意しましょう.仮説検定は「帰無仮説を棄却することで対立仮説を成立させる手法」であって「帰無仮説を採択することで帰無仮説を成立させる手法」ではないことに注意です.
つまり,今回帰無仮説を棄却できなかったからといって帰無仮説である「差はない(\(p_1= p_2\))」という仮説が正しいとは言えません.
なので今回は「”差はない”という仮説を否定できなかった」ということだけです.
まとめ
今回も長くなってしまった...
Z検定は仮説検定の基本の検定となるので,今回の記事で仮説検定の基本的な流れを抑えられると◎ですね.
- 帰無仮説は「差はない(\(p_1= p_2\))」とする
- 検定には両側検定/片側検定があり,両側検定は「差がある(\(p_1\ne p_2\))」を対立仮説にし,片側検定では「\(p_1> p_2\)」や「\(p_1< p_2\)」を対立仮説とする
- 比率の差の標本分布の平均は,それぞれの比率の標本分布の平均の差を求めればよい.
- 比率の差の標本分布の分散は,それぞれの比率の標本分布の分散の和を求めればよい.
- 最終的には標準正規分布に従う統計量を計算し,有意水準を5%とした時,両側検定なら\(z<-1.96\)もしくは\(1.96<z\)の時帰無仮説を棄却でき,片側検定なら\(1.64<z\)(もしくは\(z<-1.64\))の時に帰無仮説を棄却できる
- Pythonで比率の差の検定をするならstatsmodels.stats.proption.propotions_ztest()を使う
- 「帰無仮説が成立するという仮定のもとで今回の標本観察の結果が起こりうる確率」をp値といい,通常p値が有意水準(例えば0.05)未満かどうかで棄却するかどうかを決める
- 帰無仮説が棄却できなかったからといって,帰無仮説が正しいとすることはできない
今回も盛りだくさんでしたが,一つ一つのステップを踏めばそんなに難しくないはず!
検定はロジックが命です.全体の流れを掴める様にしておきましょう◎
追記) 次回の記事書きました.次回の記事では,検定の結果についてもう少し詳しく見ていこうと思います.「検定して終わり」ではなく,検定の結果がどういう意味なのかを詳しく理解することによって,正しく検定を使えるようになります.